1.结构动力学计算方法——达朗贝尔原理
达朗贝尔:在任一刻t,质点在主动惯性力,阻尼力及弹性恢复力三者作用下保持动力平衡。
2.结构动力学(地震)基本计算公式
(1)单自由度运动方程:
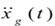 ——加速度
——加速度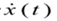 ——速度
——速度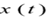 -——位移
-——位移
m—结构质量,c—结构阻尼,k—结构刚度
(2)多自由度运动方程: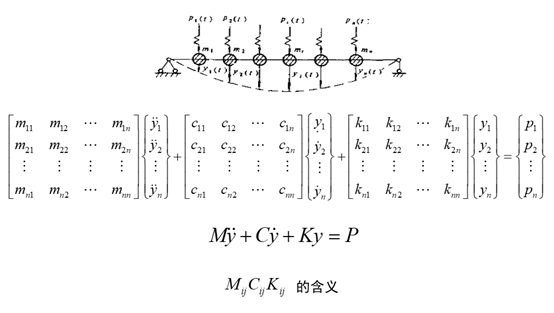
3.模态分析—自振频率及振型求解
地震有限元分析很重要的一步是要进行模态分析,分析可以得到自振频率及各阶振型,为后续的反应谱等计算提供基础参数。
模态分析不考虑阻尼的影响。原理如下:
4.反应谱的理论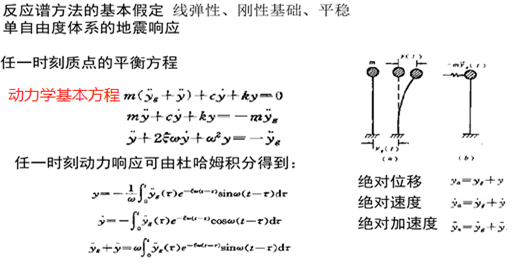
如上公式,如采用时程法则可以得到每时刻的地震响应,而我们设计时最关心的地震的最大的响应,另外对动力方程积分求解在过去计算机不算发达的时候时比较困难的,因此有了反应谱,他的原理如下:
其中:w=mg,重度重
反应谱放大系数,如下图,它是地震震级、场地条件、自振周期、特征周期及阻尼的函数。
有了反应谱放大系数就无需对动力方程进行积分计算,根据振型叠加即可求解地震响应,提高了计算速度。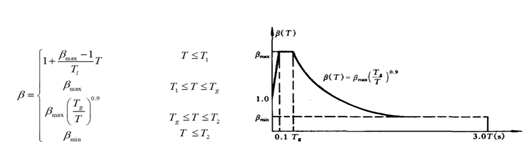
5.反应谱计算步骤(振型叠加法)
进行了模态分析后即可知结构自振周期,振型及每阶振型的参与系数,根据自振周期查取反应谱放大系数,按如下公式就可求出每个结点加速度,位移,应力及作用力,并进行组合即可得到响应,无需对动力方程进行积分计算。
其中: 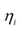 振型参与系数,
振型参与系数,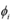 振型向量,
振型向量, 地震峰值加速度(例如7度为0.1g),其余参数意义见前述。
地震峰值加速度(例如7度为0.1g),其余参数意义见前述。
题外(振型的物理意义):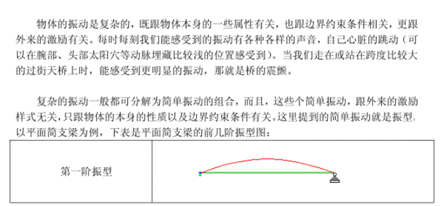
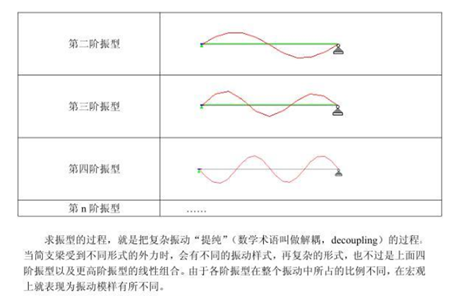
6.时程分析法
7.ansys反应谱计算实现
(1) 模态分析
边界约束
计算结果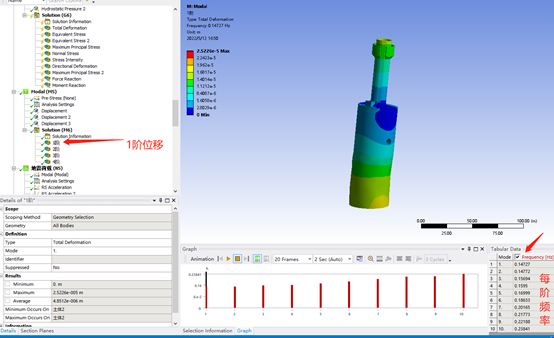
(2) 反应谱地震效应计算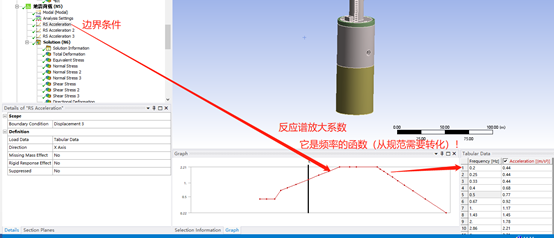
7.问题探讨
(1) 高耸结构施工偏差在地震作用下是否会放大
由地震的动力方程可知,地震响应和本身的刚度,质量及阻尼有关,施工偏差一般本身不会改变结构的刚度质量及阻尼,因此不会发生放大的作用。
(2) 塔体内的水体对地震的作用是变大还是变小
由如下的反应谱放大系数可大概可知地震响应随自振周期的变化,在自振周期小于特征周期的情况下,自振周期越大,响应越大,大于特征周期时,自振周期越大,响应反而变小,而自振周期是质量和刚度的函数,与质量成正比,考虑了水体相当于增加了结构的质量,那么自振周期是变大的,如自振周期大于特征周期,那么水体的作用将是降低结构的响应,减小结构在地震作用下的位移。

最后编辑:秦晓川 更新时间:2024-02-11 10:45
